How to Find Outliers with SQL

Use ORDER BY to find Outliers

A fast way to identify outliers is to sort the relevant values in both ascending and descending order. This allows you to quickly skim through the highest and lowest values. If you have a sense of what you are expecting from your data, this can help you quickly identify any unexpected values.

If we were looking at the ages of friends, we’d expect to see values that fall into the range of ages for adults. Let’s take a look at what we see in the example below.

To sort our values, we could use the following query.

SELECT full_name,
age
FROM friends
ORDER BY age

Here’s what a sample output could look like.

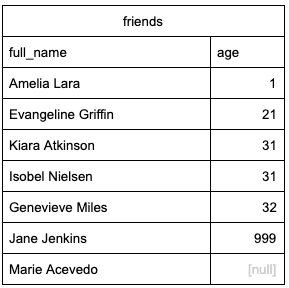
By sorting we can easily identify anomalies within the data. We don’t expect any of our friends to have an age of 1 or 999, so these outliers are likely an error. Because this is a small dataset, we can also view the final lines in our results.

If we had a larger dataset but wanted to quickly view the end of our data, we could do so by adding DESC to our ORDER BY statement.

SELECT full_name,
age
FROM friends
ORDER BY age DESC

This method can be great for identifying obvious outliers that quickly stand out. However, it may miss some other details in the data. For example, if we have less knowledge of the expected values in our dataset, there may be enough outliers that they don’t stand out with just a quick look at the high and low values.

It’s often helpful to be able to use a more statistical method for identifying outliers.

Using NTILE to find Outliers

One statistical method of identifying outliers is through the use of the interquartile range, or IQR. When we find values that fall outside of 1.5 times the range between our first and third quartiles, we typically consider these to be outliers.

SQL has a function that allows us to easily separate our values into our four quartiles. When we use NTILES() we separate our data into the same number of groups as the value inside the brackets. Therefore, if we want to separate our data into quartiles we would use NTILE(4).

NTILE is used in conjunction with a window function. If we use a similar example of friends’ ages, this is what the syntax would look like this:

SELECT
	full_name,
	age,
	NTILE(4) OVER (ORDER BY age) AS age_quartile
FROM friends

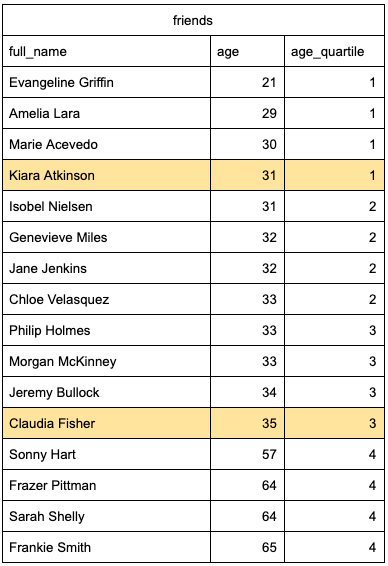
When using NTILE() in SQL, if we have an odd number of values in each of our quartiles, the maximum value in the first quartile will be the Q1 value, and the maximum value in the third quartile will be the Q3 value.

In our case, the Q1 value is 31, and the Q2 value is 35. We can easily identify these values using a subquery.

SELECT
	age_quartile,
	MAX(age) AS quartile_break
FROM(
	SELECT
    	full_name,
		age,
		NTILE(4) OVER (ORDER BY age) AS age_quartile
	FROM friends) AS quartiles
WHERE age_quartile IN (1, 3)
GROUP BY age_quartile

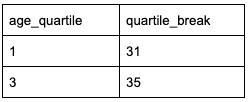
This gives us an IQR of 4, and 1.5 x 4 is 6.

To find the lower threshold for our outliers we subtract from our Q1 value:

31 - 6 = 25

To find the upper threshold for our outliers we add to our Q3 value:

35 + 6 = 41

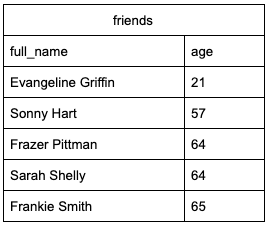
We can then use WHERE to filter values that are above or below the threshold.

SELECT full_name,
age
FROM friends
WHERE age < 25 OR age > 41

Full Query

While the above is great for explaining what we’re doing when finding outliers, it does have some issues. It works if the number of values in each half are odd, but we would need to make adjustments if it was even. Also, it requires us to write two different queries to get our results.

It can be helpful to be able to run a single query that pulls the results. Here’s one way to do that:

with orderedList AS (
SELECT
	full_name,
	age,
	ROW_NUMBER() OVER (ORDER BY age) AS row_n
FROM friends
),
iqr AS (
SELECT
	age,
    full_name,
	(
		SELECT age AS quartile_break
		FROM orderedList
		WHERE row_n = FLOOR((SELECT COUNT(*)
			FROM friends)*0.75)
			) AS q_three,
	(
		SELECT age AS quartile_break
		FROM orderedList
		WHERE row_n = FLOOR((SELECT COUNT(*)
			FROM friends)*0.25)
			) AS q_one,
	1.5 * ((
		SELECT age AS quartile_break
		FROM orderedList
		WHERE row_n = FLOOR((SELECT COUNT(*)
			FROM friends)*0.75)
			) - (
			SELECT age AS quartile_break
			FROM orderedList
			WHERE row_n = FLOOR((SELECT COUNT(*)
				FROM friends)*0.25)
			)) AS outlier_range
	FROM orderedList
)

SELECT full_name, age
FROM iqr
WHERE age >= ((SELECT MAX(q_three)
	FROM iqr) +
	(SELECT MAX(outlier_range)
		FROM iqr)) OR
		age <= ((SELECT MAX(q_one)
	FROM iqr) -
	(SELECT MAX(outlier_range)
		FROM iqr))

This query uses ROW_NUMBER and FLOOR (always rounds down) to find the Q1 (at the row 25% of the way through) and Q3 (at the row 75% of the way through) values. From there, we can calculate the IQR x 1.5 and used these as reference for our outliers.

Technical Note

The above query will be 100% accurate if each half of our data has an odd number of values. To check this, we would count the total number of rows and divide this count in half. If the result end in .5, we would round down. From there, we can determine if there are an odd or even number of values in each half.

For example, if I have a total of 55 values, half of this is 27.5. If I round down, I have 27, which is odd and therefore the query will be entirely accurate.

If the value is even, for example, I had 26 values in each half instead of 27, then I would need to adjust the query to be entirely accurate. In this case I would need the average of the 13th and the 14th values to find Q1 and similarly for Q3.

To do this, the above query can be adjusted as follows:

with orderedList AS (
SELECT
	full_name,
	age,
	ROW_NUMBER() OVER (ORDER BY age) AS row_n
FROM friends
),

quartile_breaks AS (
SELECT
	age,
    full_name,
	(
	SELECT age AS quartile_break
	FROM orderedList
	WHERE row_n = FLOOR((SELECT COUNT(*) FROM friends)*0.75)
	) AS q_three_lower,
	(
	SELECT age AS quartile_break
	FROM orderedList
	WHERE row_n = FLOOR((SELECT COUNT(*) FROM friends)*0.75) + 1
	) AS q_three_upper,
	(
	SELECT age AS quartile_break
	FROM orderedList
	WHERE row_n = FLOOR((SELECT COUNT(*) FROM friends)*0.25)
	) AS q_one_lower,
	(
	SELECT age AS quartile_break
	FROM orderedList
	WHERE row_n = FLOOR((SELECT COUNT(*) FROM friends)*0.25) + 1
	) AS q_one_upper
	FROM orderedList
	),

iqr AS (
SELECT
	age,
    full_name,
	(
	(SELECT MAX(q_three_lower)
    	FROM quartile_breaks) +
	(SELECT MAX(q_three_upper)
    	FROM quartile_breaks)
	)/2 AS q_three,
	(
	(SELECT MAX(q_one_lower)
    	FROM quartile_breaks) +
	(SELECT MAX(q_one_upper)
    	FROM quartile_breaks)
	)/2 AS q_one,
	1.5 * ((
	(SELECT MAX(q_three_lower)
    	FROM quartile_breaks) +
	(SELECT MAX(q_three_upper)
    	FROM quartile_breaks)
	)/2 - (
	(SELECT MAX(q_one_lower)
    	FROM quartile_breaks) +
	(SELECT MAX(q_one_upper)
    	FROM quartile_breaks)
	)/2) AS outlier_range
FROM quartile_breaks
)

SELECT
	full_name,
    age
FROM iqr
WHERE age >=
	((SELECT MAX(q_three)
		FROM iqr) +
	(SELECT MAX(outlier_range)
		FROM iqr))
 OR age <=
 	((SELECT MAX(q_one)
		FROM iqr) -
	(SELECT MAX(outlier_range)
		FROM iqr))

Written by: Rebecca Barnes
Reviewed by: Matt David